Enti geometrici fondamentali
INDICARE PUNTI, RETTE E PIANI
Per indicare la posizione di un punto disegniamo un puntino e lo indichiamo con una lettera in stampatello maiuscolo: A, B, C…

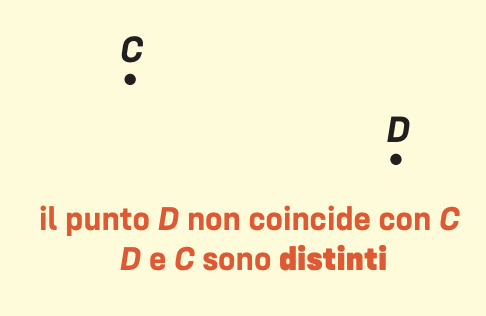
Due punti possono essere distinti o coincidenti.
Per indicare che due punti coincidono, scriviamo E ≡ F.
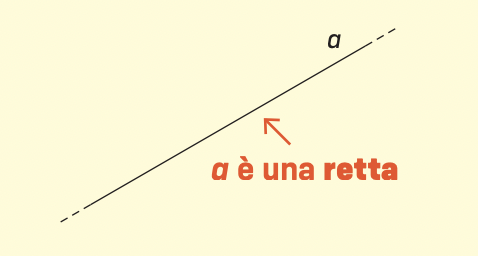
Una retta è illimitata: non ha punto di inizio né di fine.
Per questo, la disegniamo tratteggiandone le estremità.
Indichiamo le rette con le lettere minuscole: a, b, c…
Per indicare che due punti coincidono, scriviamo E ≡ F.
Una retta è illimitata: non ha punto di inizio né di fine.
Per questo, la disegniamo tratteggiandone le estremità.
Indichiamo le rette con le lettere minuscole: a, b, c…
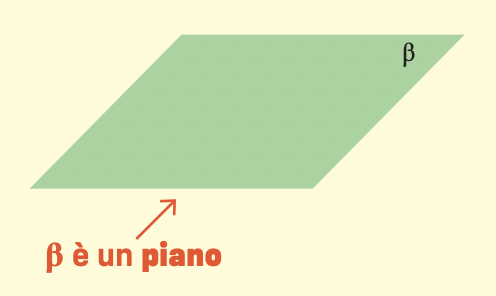
Un piano è illimitato. Nonostante questo lo rappresentiamo come una figura con lati chiusi e tratteggiati a significare che il piano si prolunga senza limiti.
Per indicare i piani si usano le lettere dell’alfabeto greco.
Per indicare i piani si usano le lettere dell’alfabeto greco.
RELAZIONI TRA PUNTI, RETTE E PIANI
Le posizioni di un punto e una retta sono due.
P è sulla retta oppure P non è sulla retta.
P è sulla retta oppure P non è sulla retta.
Per trasformare una misura espressa in metri in una espressa in decimetri devi moltiplicare per 10.
1,2 m = 12 dm
Per trasformare una misura espressa in metri in una espressa in decametri devi dividere per 10.
1,2 m = 0,12 dam
1,2 m = 12 dm
Per trasformare una misura espressa in metri in una espressa in decametri devi dividere per 10.
1,2 m = 0,12 dam
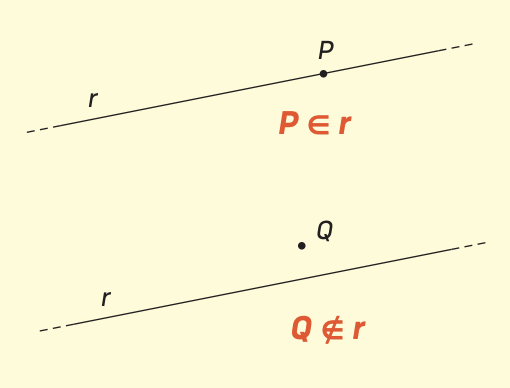
Nel primo caso il punto appartiene (∈) alla retta; nel secondo caso il punto non appartiene (∉) alla retta.
Le posizioni reciproche di due rette nel piano sono due.
Due rette r e s possono non avere nessun punto in comune.
Le rette sono parallele.
Le posizioni reciproche di due rette nel piano sono due.
Due rette r e s possono non avere nessun punto in comune.
Le rette sono parallele.
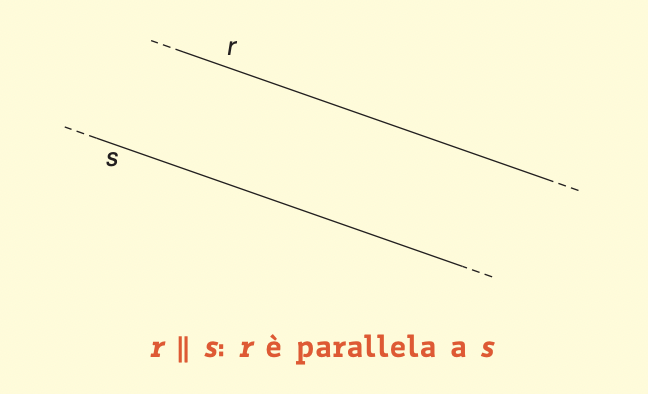
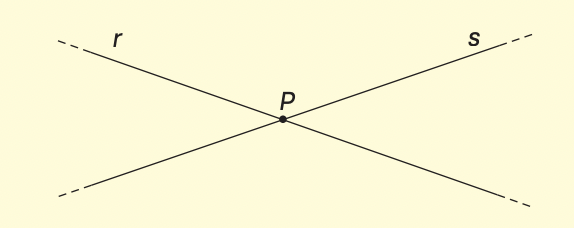
In alternativa due rette r e s hanno un solo punto in comune, che è il loro punto di incidenza o di intersezione.
Le rette sono incidenti.
Le rette sono incidenti.


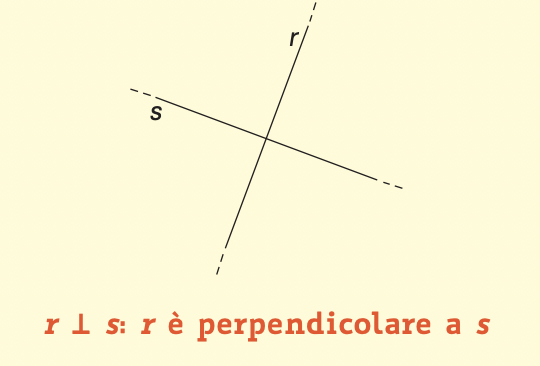
Tra tutte le rette incidenti ci sono le rette perpendicolari, che oltre a essere incidenti dividono il piano in quattro parti uguali, cioè formano quattro angoli retti.
SEMIRETTE E SEGMENTI
SEMIRETTE E SEGMENTI
Una semiretta è una parte di retta delimitata da un punto.
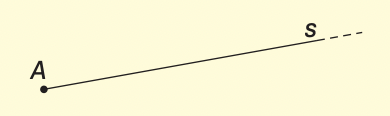
Una parte della retta compresa tra due punti A e B è il segmento AB.
I punti A e B sono gli estremi del segmento.
I punti A e B sono gli estremi del segmento.

Un punto divide una retta in due semirette opposte.

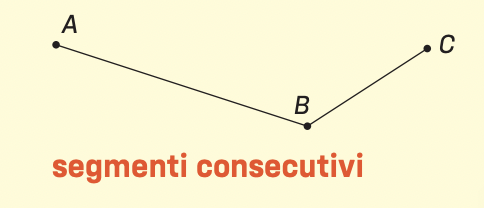
Due segmenti che hanno un estremo in comune sono consecutivi.
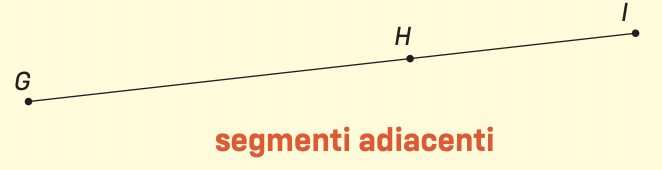
Due segmenti consecutivi che stanno sulla stessa retta sono adiacenti.
DISTANZA TRA DUE PUNTI
E TRA UN PUNTO E UNA RETTA
DISTANZA TRA DUE PUNTI
E TRA UN PUNTO E UNA RETTA
E TRA UN PUNTO E UNA RETTA
La distanza tra due punti A e B è la lunghezza del segmento AB che li unisce.
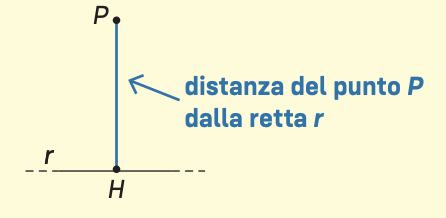
La distanza tra un punto P e una retta è la lunghezza del segmento PH perpendicolare alla retta che unisce P a un punto H della retta.
Il punto H è la proiezione del punto P sulla retta.
La distanza tra un punto P e una retta è la lunghezza del segmento PH perpendicolare alla retta che unisce P a un punto H della retta.
Il punto H è la proiezione del punto P sulla retta.
PUNTO MEDIO E ASSE DI UN SEGMENTO
PUNTO MEDIO E ASSE DI UN SEGMENTO
Il punto medio di un segmento è il punto che lo divide in due parti uguali.
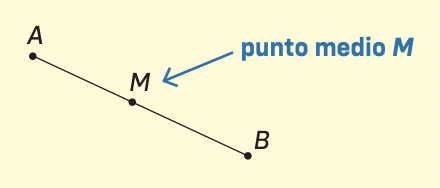
L’asse di un segmento è la retta perpendicolare al segmento che passa per il punto medio del segmento.
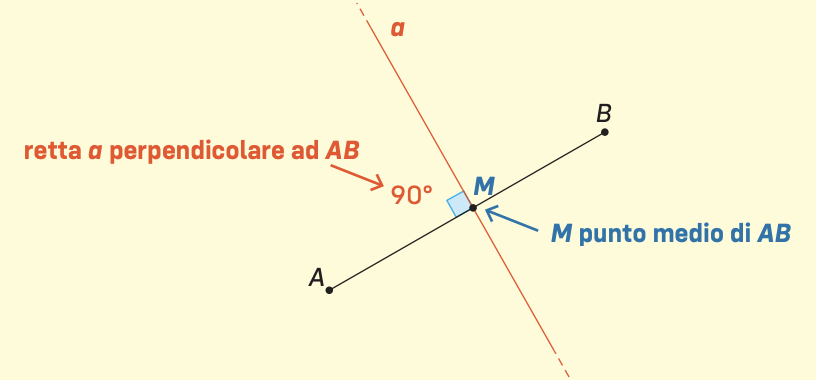
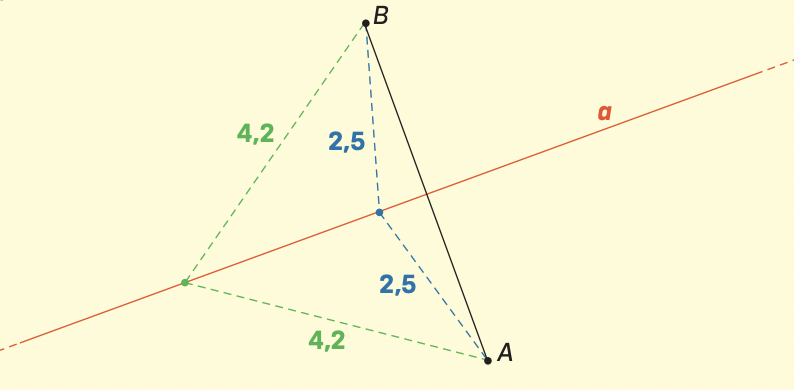
Ogni punto dell’asse di un segmento ha la stessa distanza dai due estremi del segmento.
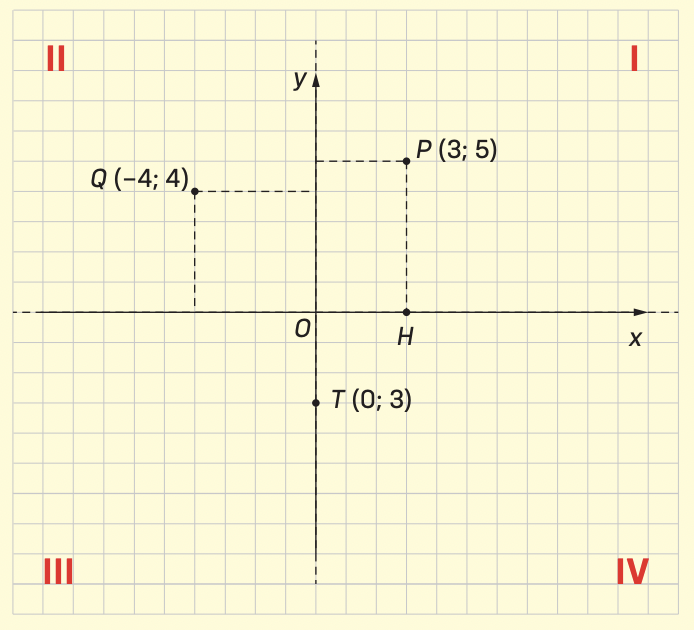
IL PIANO CARTESIANO
IL PIANO CARTESIANO
Un riferimento cartesiano è una coppia di rette perpendicolari.
Il punto in comune si chiama origine.
Il punto in comune si chiama origine.
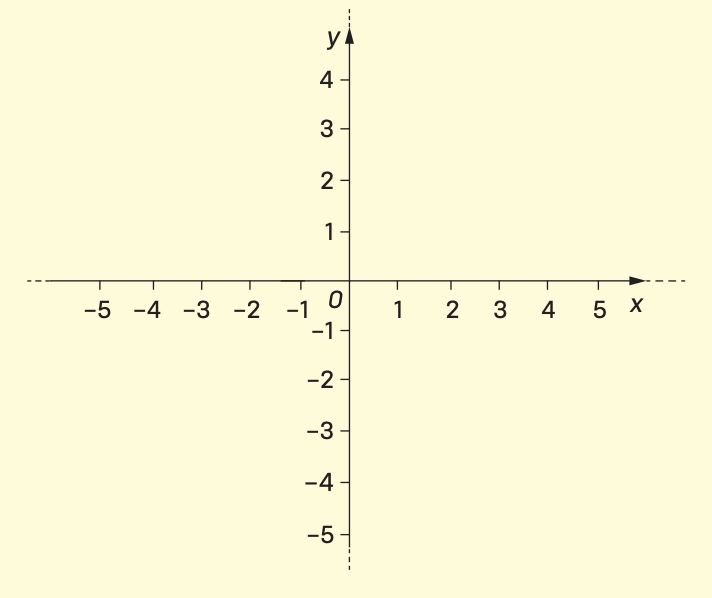
Su ciascuna retta rispetto all’origine si segnano i punti di una retta numerica.
Le due rette numeriche si chiamano assi cartesiani: asse delle ascisse (o delle x) e asse delle ordinate (o delle y).
I due assi dividono il piano in quattro quadranti: primo, secondo, terzo e quarto quadrante.
Ogni punto del piano è determinato da due coordinate.
La prima coordinata si chiama ascissa, la seconda ordinata.
L’ascissa è la distanza del punto dall’asse delle y.
L’ordinata è la distanza del punto dall’asse delle x.
Le due rette numeriche si chiamano assi cartesiani: asse delle ascisse (o delle x) e asse delle ordinate (o delle y).
I due assi dividono il piano in quattro quadranti: primo, secondo, terzo e quarto quadrante.
Ogni punto del piano è determinato da due coordinate.
La prima coordinata si chiama ascissa, la seconda ordinata.
L’ascissa è la distanza del punto dall’asse delle y.
L’ordinata è la distanza del punto dall’asse delle x.
Esempio:
I punti P, Q e T hanno queste coordinate.
P(3; 5) Q(−4; 4) T(0; −3)
P(3; 5) Q(−4; 4) T(0; −3)