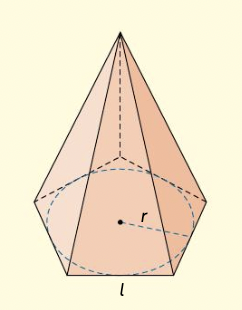
Solidi a una base
SOLIDI DI ROTAZIONE A UNA BASE: I CONI
Un cono (circolare retto) è il solido generato dalla rotazione di un triangolo rettangolo attorno a uno dei suoi cateti.
L’ipotenusa del triangolo è l’apotema del cono.Il cateto attorno a cui ruota il triangolo è l’altezza del cono e la retta che lo contiene è l’asse di rotazione.
L’altro cateto è il raggio e descrive la base che è un cerchio.
Il punto comune all’ipotenusa e all’asse di rotazione è il vertice del cono.
L’ipotenusa del triangolo è l’apotema del cono.Il cateto attorno a cui ruota il triangolo è l’altezza del cono e la retta che lo contiene è l’asse di rotazione.
L’altro cateto è il raggio e descrive la base che è un cerchio.
Il punto comune all’ipotenusa e all’asse di rotazione è il vertice del cono.
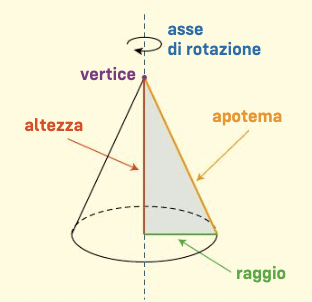
Apotema, raggio e altezza formano un triangolo rettangolo.
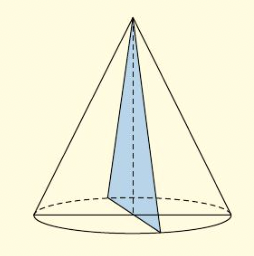
Tagliando il cono con un piano passante per l’asse di rotazione si ottiene un triangolo isoscele.
Tagliando il cono con un piano passante per l’asse di rotazione si ottiene un triangolo isoscele.
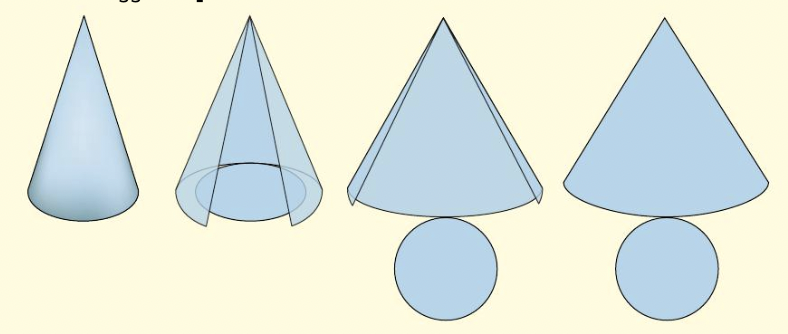
Lo sviluppo della superficie laterale di un cono è un settore circolare che ha come raggio l’apotema del cono e come arco la circonferenza di base.
Per calcolare l’area della superficie laterale del cono calcola l’area del settore circolare di raggio a e arco 2πr.
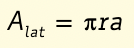
Per calcolare il volume moltiplica l’area del cerchio di base per l’altezza del cilindro.
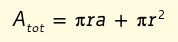
Per calcolare il volume del cono ricorda che è un terzo di quello del cilindro con stessa base e stessa altezza:
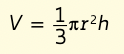
Tra tutti i coni, c’è il cono equilatero nel quale l’apotema è congruente al diametro di base.
La sezione del cono equilatero ottenuta con un piano passante per l’asse di rotazione è un triangolo equilatero
La sezione del cono equilatero ottenuta con un piano passante per l’asse di rotazione è un triangolo equilatero
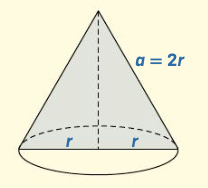
Le tre misure complessive del cono equilatero sono:
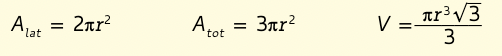
POLIEDRI A UNA BASE: LE PIRAMIDI
I poliedri a una base si chiamano piramidi.
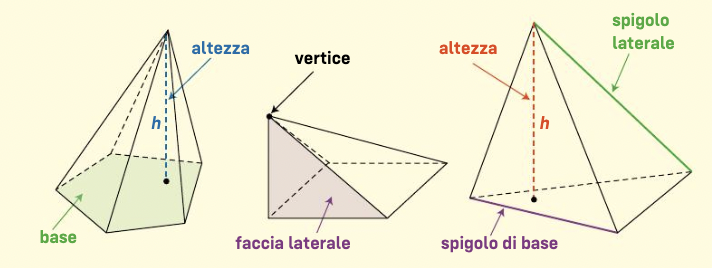
Una piramide è un poliedro a una base. La base è un poligono.
Le altre facce (laterali) sono triangoli e hanno un vertice in comune: il vertice della piramide.
Le facce laterali compongono la superficie laterale.
Gli spigoli laterali sono i segmenti che uniscono il vertice della piramide a quelli della base.
La distanza del vertice dal piano della base è l’altezza della piramide. Il punto in cui l’altezza incontra il piano di base si chiama piede dell’altezza.
Una piramide è un poliedro a una base. La base è un poligono.
Le altre facce (laterali) sono triangoli e hanno un vertice in comune: il vertice della piramide.
Le facce laterali compongono la superficie laterale.
Gli spigoli laterali sono i segmenti che uniscono il vertice della piramide a quelli della base.
La distanza del vertice dal piano della base è l’altezza della piramide. Il punto in cui l’altezza incontra il piano di base si chiama piede dell’altezza.
Tra tutte le piramidi, ce ne sono alcune con cui è più facile lavorare: le piramidi rette.
Una piramide retta è una piramide in cui la base è circoscrivibile e il piede dell’altezza è il centro della circonferenza inscritta nella base. Le altezze delle facce laterali prendono il nome di apotema della piramide.
L’altezza della piramide, il raggio della circonferenza inscritta nella base e l’apotema (l’altezza delle facce laterali) della piramide formano un triangolo rettangolo e sono legati dal teorema di Pitagora.Grazie a questo si può verificare che le altezze delle facce laterali sono tutte uguali.
Una piramide retta è una piramide in cui la base è circoscrivibile e il piede dell’altezza è il centro della circonferenza inscritta nella base. Le altezze delle facce laterali prendono il nome di apotema della piramide.
L’altezza della piramide, il raggio della circonferenza inscritta nella base e l’apotema (l’altezza delle facce laterali) della piramide formano un triangolo rettangolo e sono legati dal teorema di Pitagora.Grazie a questo si può verificare che le altezze delle facce laterali sono tutte uguali.
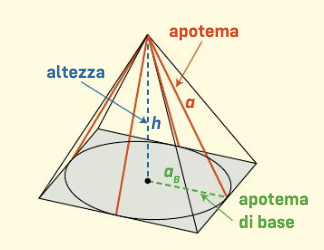
Attenzione! Anche il raggio della circonferenza inscritta prende il nome di apotema (del poligono di base). In questo caso, per distinguerlo dall’apotema della piramide lo chiameremo apotema di base.
Per calcolare l’area della superficie laterale ricorda che è equivalente a un triangolo che ha come base il perimetro di base e come altezza l’apotema:
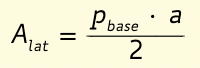
Per calcolare l’area della superficie totale aggiungi l’area della base:
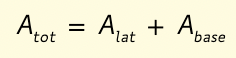
Per calcolare il volume della piramide (anche non retta) considera che è equivalente a un terzo del prisma che ha la stessa base e la stessa altezza:
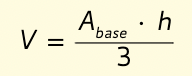
Una piramide regolare è una piramide retta che ha per base un poligono regolare.