Grandezze inversamente proporzionali
Quando due grandezze si dicono inversamente proporzionali?
Due grandezze variabili sono inversamente proporzionali se raddoppiando, triplicando la variabile indipendente x, la variabile dipendente y si dimezza, diventa un terzo; analogamente se la prima si dimezza, diventa un terzo, la seconda diventa il doppio, il triplo.
Due grandezze x e y sono inversamente proporzionali se il prodotto di due valori corrispondenti si mantiene costante:
y · x = k
con k > 0; k è il coefficiente di proporzionalità inversa
La funzione di proporzionalità inversa si esprime con l’equazione: y = k/ x
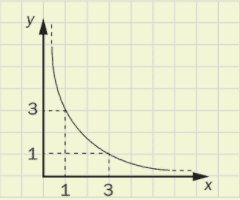
il cui grafico è un ramo di iperbole equilatera:
se k = 3 y = 3/x
Esempio
I valori di due grandezze variabili riferite a due situazioni diverse sono riportati nelle seguenti tabelle.
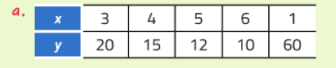
Nella prima tabella i prodotti di valori corrispondenti sono tutti uguali:
3 × 20 = 4 × 15 = 5 × 12 = 6 × 10 = 1 × 60 = 60
Le due grandezze x e y sono inversamente proporzionali.
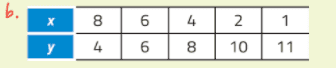
Nella seconda tabella i prodotti di valori corrispondenti non sono tutti uguali: 8 × 4 ≠ 6 × 6
Le due grandezze non sono inversamente proporzionali.

